Cerne Group-Research

In addition to providing new challenges to our basic understanding condensed matter physics, strange metals such as magnetic oxides and high temperature superconductor cuprates as well as magnetic semiconductors hold great technological promise. By exploring the polarization of transmitted and reflected infrared light induced by a magnetic field, we can find new structure that is hidden from more conventional measurements.

Left to right: Chase Ellis, Alex Carson (undergrad), Alok Mukherjee, John Cerne, Nada Tesarova, and Chris Smith (undergrad) in the lab.

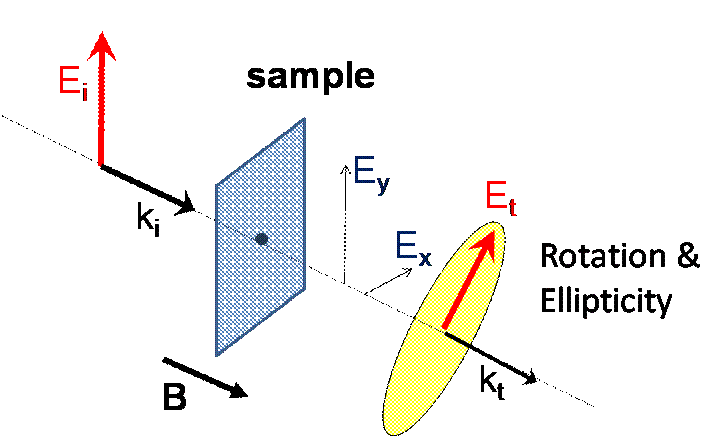
What we measure. The cartoon above shows the changes in the polarization of transmitted light that samples produce when a magnetic field is applied. This technique measures both the rotation and ellipticity of the transmitted light as a function of IR frequency.

In addition to providing new challenges to our basic understanding of materials, strange metals (such as ruthenate oxides and high temperature superconductors) and magnetic semiconductors hold great technological promise. By exploring how polarization (the direction in which the electric field in a light wave oscillates) of transmitted and reflected infrared light changes in a magnetic field, we find new structure that is hidden from more conventional measurements, such as infrared spectroscopy, which only measures the intensity (the amplitude of the electric field in a light wave) of transmitted and reflected light.

These materials have a number of fundamentally anomalous properties that have defied explanation for the last decade. One of the most striking anomalies in these sytems is the DC Hall effect. A rich variety of models have been used to explain the DC Hall measurements in these materials, however, these models predict different behavior at higher frequencies. Thus, Hall measurements at finite frequencies are essential for determining which models have the most promise for providing a complete understanding of these materials. We have extended Hall measurement into the infrared frequency range by using sensitive optical polarization modulation techniques.

Two of the most fundamental measurements in condensed matter physics are the dc Hall effect and infrared spectroscopy. In metals and semiconductors, the dc (direct current, meaning constant current) Hall effect allows one to determine the sign and density of the charge carriers. This in turn allows one to determine the dc mobility of the material, which is critical for making fast electronic devices. The dc Hall effect has also been critical in the discovery of many interesting phenomena in both conventional and unconventional materials. The discoveries of the integer and fractional quantum Hall effects in semiconductors have led to two Nobel prizes in the last few decades. The dc Hall effect in high temperature superconductor cuprates (HTSC) has exhibited strikingly anomalous behavior that remains one of the key puzzles in understanding these materials. The many interesting metallic ferromagnets such as Ca_xSr_1-xRuO₃ and diluted magnetic semiconductors (DMS), the origin of the anomalous dc Hall effect remains unclear on a fundamental level.

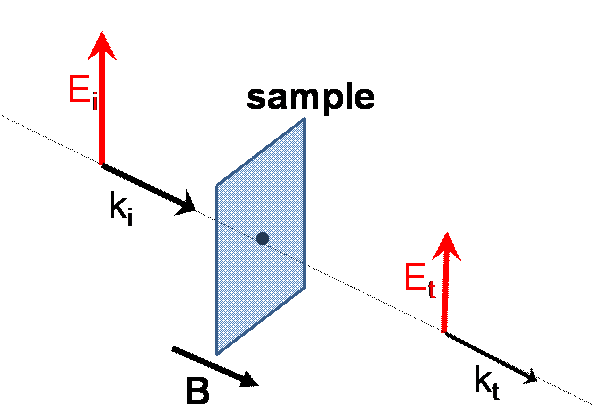
A simplified cartoon explaining the dc Hall effect measurement is shown in the left panel of the figure below. An electric field E_y is applied in the y-direction to drive a current I in the same direction through the sample in the presence of a magnetic field B, which is oriented along the z-direction and is perpendicular to the surface of the sample. The interaction of the current and the magnetic field leads to an electric field E_x in the x-direction, which in produces a Hall voltage V_Hall, which is also across the x-direction. The dc Hall effect essentially measures how charged carriers are deflected by a magnetic field.

test3 DC Hall effect: The current I interacts with the applied magnetic field B to produce an electric field Ex and Hall voltage VHall that are along the x-direction.	IR conductivity: Infrared radiation provides an oscillating electric field Ei, which interacts with the sample. There may or may not be an applied magnetic field B, and only the magnitude of the transmitted and/or reflected light is measured.	IR Hall effect: Light that is linearly polarized in the vertical direction with electric field Ei is incident upon the sample from the left. The sample in magnetic field B produces a tranverse component Ex which adds to the longitudinal component to produce a new polarization which is rotated and elliptical.

Unlike dc measurements, where the applied electric field is constant, infrared (IR) conductivity measurements probe the dynamic response of the sample using an oscillating electric field. A simple cartoon representing an IR conductivity measurement is shown in the middle panel of the figure above. The oscillating electric field is provided by IR radiation, with wavelengths typically ranging from 1 μm to tens of μm. By measuring the magnitude of the transmitted electric field, E_t, as a function of frequency, one gains important information about the energy levels in the sample that are absorbing the light. The IR range is important for many materials because there are many fundamental excitations due to the band structure and/or collective effects that lie in this energy range. There may or may not be an applied magnetic field B, and only the magnitude of the transmitted light is measured. The polarization of the transmitted light may change, but this technique is not sensitive to these changes.

IR Hall effect measurements combine the sensitivity to the carriers' tranverse response of the Hall effect with the energy resolution of ir conductivity measurements to provide a new view into materials. A simple cartoon representing an IR Hall measurement is shown in the right panel of the figure above. Light that is linearly polarized in the vertical direction with electric field Ei is incident upon the sample from the left. The sample in magnetic field B produces a tranverse component Ex (just like the dc Hall effect!) which adds to the longitudinal component to produce a new polarization which is rotated and elliptical. This rotation and ellipticity are measured as a function of frequency and can reveal smaller aysmmetries in the sample's response that would not be observed using conventional IR conductivity measurements. One key advantage of IR Hall measurements is that unlike IR conductivity measurements which measure the sum of the sample's response to left and right circularly polarized light, this technique measures the difference. Therefore, small asymmetries and small changes in the electronic structure of the sample can be seen much more clearly with IR Hall measurements.

The cartoon below shows the changes in the polarization of transmitted light that samples produce when a magnetic field is applied. For more background on the polarization of light and polarization-sensitive measurement, please take a look at Conceptual Learning Approach to Waves.

The new measurement and analysis techniques that we have developed allow us to extract both the infrared (1-11 μm wavelength light) longitudinal conductivity σ_xx, which describes how charges move along an applied electric field, as well as the Hall conductivity σ_xy, which describes how charges move perpendicular to an applied electric field in the presence of a magnetic field, by measuring the polarization of light (Kim et al., Phys. Rev B 75, 214416 (2007)). These measurement and analysis techniques have been applied to study diluted magnetic semiconductors, magnetic oxides, and high temperature superconducting cuprates. These measurements are still in their early stages, but we expect to gain more insight and begin looking at other materials in the near future.

Diluted Magnetic Semiconductors

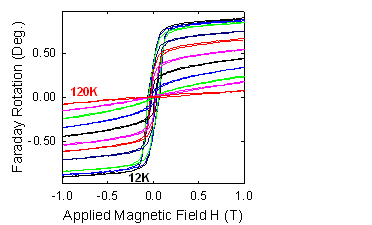
Ga_1-xMn_xAs is an exciting material because it raises interesting fundamental questions about magnetic semiconductors and has the potential to lead to important new technologies based on spintronics. One of the key questions in this material is the location of the Fermi level. Until this basic question is answered, it will be difficult to make further progress in understanding and manipulating this material. We have measured the polarization rotation and ellipticity in transmitted (Faraday effect) and reflected (Kerr effect) light in many different Ga_1-xMn_xAs films. The samples are from V. Novak's group in the Czech Republic, O. Dubon's group at U. of California, Berkeley, and H. Luo's group at UB. We found large Faraday and Kerr signals with hysteretic behavior (see figure below). The signals show strong frequency dependence, including sign changes. The frequency dependence in several samples at low temperature is in good agreement with calculations by the Sinova group at Texas A&M. Unlike the findings of the work by Basov and Burch (for example see, Phys. Rev. Lett 97, 087208 (2006)), our results are consistent with the Fermi level being located in the valence band and not in an impurity band. Our measuremennts can test this model very sensitively and the key test will be to look at the shifts in the Faraday and Kerr spectra as a function of carrier concentration. We have published preliminary results in the following papers:

'Infrared Magneto-Optical Studies in Ga_1-xMn_xAs Films,' G.Acbas, J. Cerne, M.Cukr, V. Novak and J. Sinova, AIP Conference Proceedings 893 (Pt. B, Physics of Semiconductors, Part B), 1217-1218 (2007).

'A Comparison of the mid-infrared magneto-optical response of Ga_1-xMn_xAs films grown by molecular beam epitaxy and ion implantation/laser melting,' G. Acbas, J. Cerne, J. Sinova, M.A. Scarpulla, O.D. Dubon, M. Cukr, and V. Novak, J. Supercond. Nov. Magn. 20, 457-460 (2007).

Magnetic Oxides

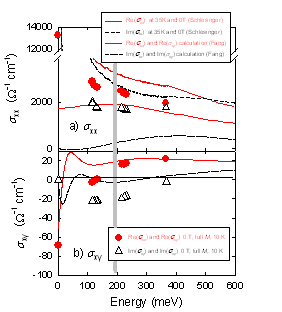
As with Ga_1-xMn_xAs, in SrRuO₃ we measured large Faraday and Kerr signals with hysteretic behavior and strong frequency dependence, including sign changes (see figure below). The Ca_xSr_1-xRuO₃ films were grown and characterized by the Christen and Mandrus groups at Oak Ridge National Lab. σ_xx determined using the Faraday/Kerr analysis is in good agreement with longitudinal transport measurements, Kostic PRL '98, and σ_xy in reasonably good agreement with predictions (Fang Science '03) above 200 meV. Below 200 meV, the infrared Hall angle has similar temperature dependence as the dc Hall angle, changing sign at approximately 140K. Above 200 meV the infrared Hall angle behaves more like the magnetic susceptibility as a function of temperature and monotonically decreases without changing sign. We have completed a preprint on the SrRuO₃ results and are analyzing them using both intrinsic and extrinsic anomalous Hall effect models. It appears that the extrinsic contribution can be tuned out by probing the Hall response at frequencies above the impurity scattering rate.

In CaRuO₃, which is the paramagnetic cousin of SrRuO₃, we measured much weaker Faraday signals that are linear in applied magnetic field. Unlike SrRuO₃, the frequency dependence of the Faraday angle in CaRuO₃ was remarkably weak in the 100-200 meV range. Although the dc Hall angle in both CaRuO₃ and SrRuO₃ changes sign with temperature, no sign change in the IR Hall angle in the 100-200 meV range was observed for CaRuO₃. The IR Hall angle in CaRuO₃ behaves like the magnetic susceptibility as a function of temperature and unlike SrRuO₃ there is no sign change as a function of temperature at 100 meV.

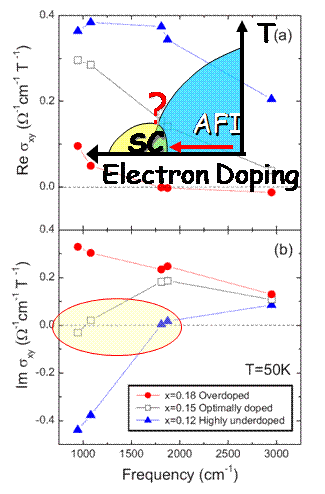
High Temperature Superconducting Cuprates

In a collaboration with the Drew (U. Maryland) and Millis (Columbia U.) groups we have explored the IR Hall conductivity σ_xy in the superconductor Pr_2-xCe_xCuO₄ (see figure below and Zimmers et al., Phys. Rev. B 76, 064515 (2007)). One of the key questions in these materials is whether there are any remnants of the antiforromagnetic insulating (AFI) state as the material is doped with electrons into the superconducting state (see top panel of figure below). Up to now, different measurement techniques have led to different answers to this important basic question. We looked at three samples that were grown by the Greene group at U. Maryland: an underdoped sample with doping concentration x=0.12, an optimally doped (has highest superconducting transition temperature) sample with doping concentration x=0.15, and an overdoped sample with doping concentration x=0.18. Since σ_xy is sensitive to small differences in the chirality (left or right handedness) of absorption of IR light, dramatic gap-like features evidenced by Im(σ_xy) crossing zero (x=0.12 and 0.15 samples in the bottom panel of the figure below) are clearly seen even for optimally doped Pr_2-xCe_xCuO₄. This is the first direct optical evidence that the AFI state is still present even for samples that have the highest superconducting temperature. The overdoped (x=0.18) sample also shows unusual behavior, which is currently being investigated.

We gratefully acknowledge the support of the Research Corporation (Cottrell Schollar Award) and the National Science Foundation (CAREER-DMR0449899) for making this work possible.